How can I find the total number of irreducible representations corresponding to the k-points?

Yachao_su

Hi all,

According to the CRYSTAL manual, for optimal parallel performance when using Pcrystal, the number of MPI processes should ideally not exceed the total number of irreducible representations associated with the k-points (assuming symmetry is applied).

However, after going through the output file from a recent run, I wasn’t able to find this number explicitly printed.Would there be a recommended way to extract or compute this value within CRYSTAL?
Or is it typically something one estimates manually based on the symmetry and k-point grid? Any guidance would be greatly appreciated!

GiacomoAmbrogio

Hi Yachao_su,

The relation you mention between MPI processes and efficiency is correct, but a bit of clarification might be necessary:limitations on efficiency apply only to the linear algebra steps and the density matrix construction (specifically, the FDIK and PDIG steps) during the SCF procedure.

In the FDIK section we are essentially diagoalizing a set of Fock matrices (of size n atomic orbitals x n atomic orbitals), one for each k point. When using symmetry-adapted Bloch functions, these matrices become block-diagonal, and each block corresponds to an irreducible representation (irrep). These blocks can then be diagonalized independently (by different MPI processes).

Diagonalization scales cubically with matrix size. However, for small systems, this time is usually negligible compared to other SCF steps. So in such cases, there's no need to worry too much about how many MPI processes you're using.

The other most time-consuming part is the computation of two-electron integrals (SHELLXN step), which scales almost linearly with system size and is not affected by the MPI-per-irrep limitation.

The limitation becomes relevant when dealing with large systems, where the irreps (ie, the block sizes) are large. In that case, the time spent on FDIK and PDIG becomes significant. Since Pcrystal cannot assign more than one MPI process per irrep, any additional processes will stay idle during diagonalization, but they are still used in other parts of the calculation.

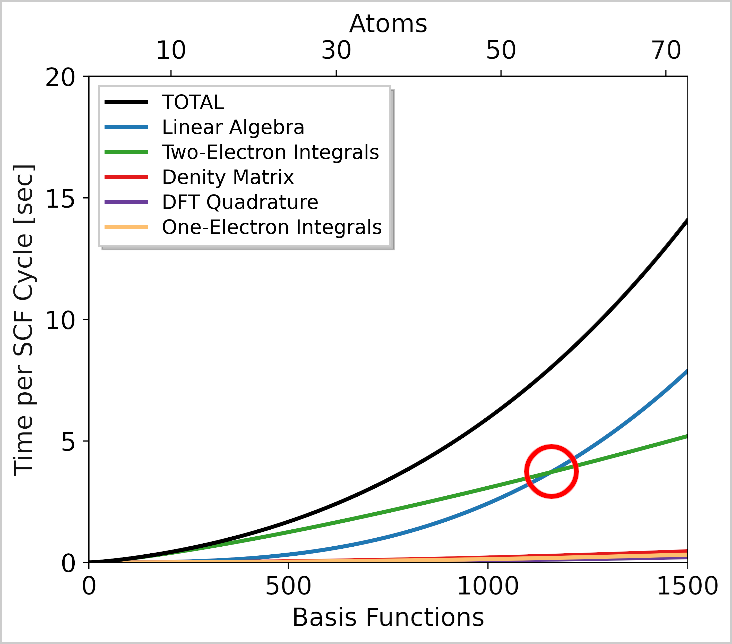
Here, I've reported an example. You can see the blue line (FDIK, i.e., diagonalization) is negligible on the left (small systems) but becomes dominant on the right (larger systems). So the MPI limitation becomes noticeable only in that region.

If you're on the right side of the plot, where the time spent in FDIK exceeds that of other steps like SHELLXN or NUMDFT (DFT integration), you should limit your number of MPI processes using the rule:

$$ \text{max MPI processes} = \sum_\mathbf{k} n_{irreps, \mathbf{k}} \times n_{spin}$$

That is, the total number of processes should not exceed the sum of all irreps across all k points, multiplied by the number of spins (2 if you're doing a spin-polarized calculation, 1 for close shell).

By default, the number of irreps is not printed in the output file. However, you can activate some advanced printing options to display this information. To do so, insert the following into the third block of your input file:

KSYMMPRT
SETPRINT
1
47 nk

Here, nk is the maximum number of k points for which you want to print symmetry information. Likely this will be the number of k points in your calculation.

You can find some reference about this option in the CRYSTAL User Manual, at pages 117-118.

The output will look like this:

 +++ SYMMETRY ADAPTION OF THE BLOCH FUNCTIONS +++

 SYMMETRY INFORMATION:
 K-LITTLE GROUP: CLASS TABLE, CHARACTER TABLE.
 IRREP-(DIMENSION, NO. IRREDUCIBLE SETS)
 (P, D, RP, RD, STAND FOR PAIRING, DOUBLING, REAL PAIRING AND REAL DOUBLING
 OF THE IRREPS (SEE MANUAL))

 K[   1] (  0  0  0)                                                    <------ 1st k point

 CLASS | GROUP OPERATORS (COMPLEX PHASE IN DEGREES)
 ------------------------------------------------------------------------
   2   |   2(   0.0);
   3   |   3(   0.0);   4(   0.0);
   4   |   5(   0.0);   6(   0.0);
   5   |   7(   0.0);   8(   0.0);   9(   0.0);
   6   |  10(   0.0);  12(   0.0);  11(   0.0);

 IRREP/CLA     1     2     3     4     5     6
 ---------------------------------------------
  MULTIP |     1     1     2     2     3     3
 ---------------------------------------------
      1  |  1.00  1.00  1.00  1.00  1.00  1.00
      2  |  1.00 -1.00  1.00 -1.00 -1.00  1.00
      3  |  2.00  2.00 -1.00 -1.00  0.00  0.00
      4  |  1.00  1.00  1.00  1.00 -1.00 -1.00
      5  |  2.00 -2.00 -1.00  1.00  0.00  0.00
      6  |  1.00 -1.00  1.00 -1.00  1.00 -1.00

   1-(1,  27);   2-(1,  25);   3-(2,  37);   4-(1,  23);   5-(2,  37);  <------ This is the information about
   6-(1,  25);                                                          <------ the irreps

 K[   2] (  1  0  0)                                                    <------ 2nd k point.

 CLASS | GROUP OPERATORS (COMPLEX PHASE IN DEGREES)
 ------------------------------------------------------------------------
   2   |  11(   0.0);

 IRREP/CLA     1     2
 ---------------------
  MULTIP |     1     1
 ---------------------
      1  |  1.00  1.00
      2  |  1.00 -1.00

   1-(1, 126);   2-(1, 122);                                             <------ irreps of 2nd k point
....

For example, here the first k point is adapted in 6 different irreps, while the second in 2

Please note: this feature should be run using one single MPI process.

Yachao_su

Thank you very much for the detailed explanation—this really helped clarify things for me! The plot and your explanation made it all very clear.